1 Answer

Zhomart · Answer 1 · 2023-03-07T15:59:44+0000

To calculate the area of the triangle we need the length of the base and the height, being the height perpendicular to the base.

The base of the triangle has a length that is equal to the diameter of the circle. It can also be expressed as 2 times the radius r. So the base is:

$b=2\cdot r=2\cdot4=8\operatorname{cm}$

The height is the segment perpendicular to the base that goes up to the vertex at the top. as it goes from the center of the circle to the border of the circle, it has a length that is equal to the radius r:

$h=r=4\operatorname{cm}$

Then, we can calculate the area of the triangle as:

$A=(b\cdot h)/(2)=(8\cdot4)/(2)=(32)/(2)=16\operatorname{cm}^2$

We can calculate the area of the circle as:

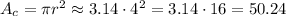
$A_c=\pi r^2\approx3.14\cdot4^2=3.14\cdot16=50.24$

The probability that a randomly selected point within the circle falls in the white area is equal to the ratio of white area to the area of the circle.

The white area is equal to the area of the circle minus the area of the triangle.

Then, we can calculate the probability as:

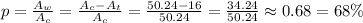
$p=(A_w)/(A_c)=(A_c-A_t)/(A_c)=(50.24-16)/(50.24)=(34.24)/(50.24)\approx0.68=68\%$

Answer: The probability is p=0.68.

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions