Question

There are two jobs you can apply for. the first job pays $22,000 the first year, with raises of $4,000 each year thereafter. the second job pays $26,000 the first year with raises of $2,000 each year thereafter. when would you make as much money in the first job as in the second?

Answer 1

We let the number of years that the two jobs will have the same payment be denoted as t. Equating the wages of these two jobs after t - 1 years will give us an equation of,
22,000 + 4000(t -1) = 26,000 + 2000(t - 1)
The value of t from the generated equation is 3. Therefore, after 3 years the jobs will be paying the same wages.

Answer 2

Answer: 3rd year

Explanation:

Given : There are two jobs you can apply for.

Let x be the time (in years).

The first job pays $22,000 the first year, with raises of $4,000 each year thereafter.

Then, the amount earned in x years by first job can be written as :-

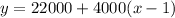`y=22000+4000(x-1)`...................(1)

The second job pays $26,000 the first year with raises of $2,000 each year there after.

Then, the amount earned in x years can be written as :-

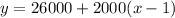`y=26000+2000(x-1)`...........................(2)

From equation (1) and (2) , we have

`22000+4000(x-1)=26000+2000(x-1)\\\\\Rightarrow\ 4000(x-1)-2000(x-1)=26000-22000\\\\\Rightarrow\ 2000(x-1)=4000\\\\\Rightarrow\ x-1=(4000)/(2000)=2\\\\\Rightarrow\ x=2+1=3`

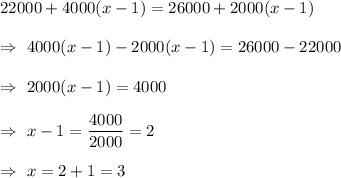
Hence, in 3rd year you would make as much money in the first job as in the second.