We can express this question as follows:
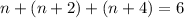
Now, we can sum the like terms (n's) and the integers in the previous expression. Then, we have:
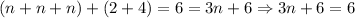
Then, to solve the equation for n, we need to subtract 6 to both sides of the equation, and then divide by 3 to both sides too:
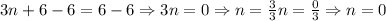
Then, we have that the three consecutive even integers are:
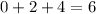
Therefore, the least integer is 0.