Question

Find the direction of the vector A⃗ = (5.1 m )x^ + (-1.5 m )y^.Find the direction of the vector B⃗ = (-1.5 m )x^ + (5.5 m )y^Find the magnitude of the vector A⃗ +B⃗ .Find the direction of the vector A⃗ +B⃗ .

Answer 1

The angle between the components x and y of a vector is given by:

`\theta=\tan ^(-1)(\frac{v_x_{}_{}}{v_y})`

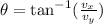
once we know this we need to find in which quadrant the vector lies so we know how to calculate the correct direction.

Vector A lies in the fourth quadrant this means that we need to subtract theta to 360° in order to get the direction of the vector, then we have:

`360-\tan ^(-1)((1.5)/(5.1))=343.61`

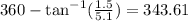
Therefore the direction of vector A is 343.61°

Vector B lies in the second quadrant, this means that we need to subtract theta (given by the first equation) to 180° in order to get the direction, then we have:

`180-\tan ^(-1)((5.5)/(1.5))=105.26`

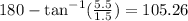
Therefore the direction of vector B is 105.26°

Let's find vector A+B:

`\begin{gathered} \vec{A}+\vec{B}=\langle5.1,-1.5\rangle+\langle-1.5,5.5\rangle \\ =\langle5.1-1.5,-1.5+5.5\rangle \\ =\langle3.6,4\rangle \end{gathered}`

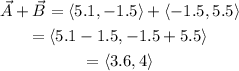
Then we have that:

`\vec{A}+\vec{B}=\langle3.6,4\rangle`

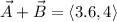
To find its magnitude we have to remember that the magnitude of any vector is given by:

`\lvert\vec{v}\rvert=\sqrt[]{v^2_x+v^2_y}`

Then for vector A+B we have:

`\begin{gathered} \lvert\vec{A}+\vec{B}\rvert=\sqrt[]{(3.6)^2+(4)^2} \\ =5.38 \end{gathered}`

Therefore the magnitude of vector A+B is 5.38 meters.

Vector A+B lies in the first quadrant, then its direction is given by the expression for theta, then we have:

`\tan ^(-1)((4)/(3.6))=48.01`

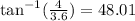
Therefore the direction of vector A+B is 48.01°