Question

Consider the graph shown. Which ordered pairs are on the inverse of the function? Check all that apply.

Answer 1

Notice that the graph of the function is a cubic polynomial. Also, the graph is moved one unit upwards, then, the function f(x) is:

`f(x)=x^3+1`

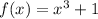
now, we can see from the y and x intercepts, that if we evaluate x= 0 and x = 1, we get:

`\begin{gathered} f(0)=-1 \\ f(1)=0 \end{gathered}`

then, applying the inverse function on both sides (we can do this since f(x) is a polynomial function and they always have inverse function), we get the following:

`\begin{gathered} f^(-1)(f(0))=f^(-1)(-1) \\ \Rightarrow0=f^(-1)(-1) \end{gathered}`

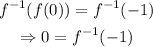
we can see that the first point that is on the graph of the inverse function is (-1,0). Doing the same on the second equation, we get:

`\begin{gathered} f^(-1)(f(1))=f^(-1)(0) \\ \Rightarrow f^(-1)(0)=1 \end{gathered}`

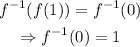
thus, the points that lie on the inverse function are (-1,0) and (0,1)