Question

PLS HELP Quadrilateral ABCD is located at A(-2, 2), B(-2, 4), C(2, 4), and D(2, 2). The quadrilateral is then transformed using the rule (x + 7, y - 1) to form the imagecoordinates of A', B', C', and D'? Describe what characteristics you would find if the corresponding vertices were connected with line segments

Answer 1

Given:

The coordinates of Quadrilateral ABCD is A(-2, 2), B(-2, 4), C(2, 4), and D(2, 2).

The quadrilateral is transformed with the rule,

`(x,y)\rightarrow\mleft(x+7,y-1\mright)`

It becomes,

`\begin{gathered} A\mleft(-2,2\mright)\rightarrow A^(\prime)\mleft(-2+7,2-1\mright)=A^(\prime)(5,1) \\ B\mleft(-2,4\mright)\rightarrow B^(\prime)(-2+7,4-1)=B^(\prime)(5,3) \\ C\mleft(2,4\mright)\rightarrow C^(\prime)(2+7,4-1)=C^(\prime)(9,3) \\ D(2,2)\rightarrow D^(\prime)(2+7,2-1)=D^(\prime)(9,1) \end{gathered}`

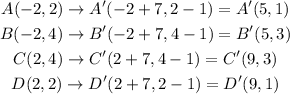
Now, join the corresponding vertices of both the quadrilateral with the line segment.

After joining the vertices of the quadrilateral ABCD and A'B'C'D'. it gives the 3-dimensional shape- a rectangular prism.