Question

Sally Sue had spent all day preparing for the prom. All the glitz and the glamour of the evening fell apart as she stepped out of the limousine and her heel broke and she fell to the ground. Within minutes, news of her crashing fall had spread to the 550 people already at the prom. The function, p(t) = 550(1-e^-0.039t) where t represents the number of minutes after the fall, models the number of people who were already at the prom who heard the news.How many minutes does it take before all 550 people already at the prom hear the news ofthe great fall? Show your work.

Answer 1

We have the function

`p(t)=550(1-e^(-0.039t))`

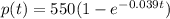
Therefore we want to determine when we have

`p(t_0)=550`

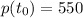
It means that the term

`e^(-0.039t)`

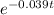
Must go to zero, then let's forget the rest of the function for a sec and focus only on this term

`e^(-0.039t)\rightarrow0`

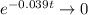
But for which value of t? When we have a decreasing exponential, it's interesting to input values that are multiples of the exponential coefficient, if we have 0.039 in the exponential, let's define that

`\alpha=(1)/(0.039)`

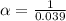
The inverse of the number, but why do that? look what happens when we do t = α

`e^(-0.039t)\Rightarrow e^(-0.039\alpha)\Rightarrow e^(-1)=(1)/(e)`

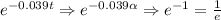
And when t = 2α

`e^(-0.039t)\Rightarrow e^(-0.039\cdot2\alpha)\Rightarrow e^(-2)=(1)/(e^2)`

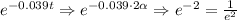
We can write it in terms of e only.

And we can find for which value of α we have a small value that satisfies

`e^(-0.039t)\approx0`

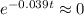
Only using powers of e

Let's write some inverse powers of e:

`\begin{gathered} (1)/(e)=0.368 \\ \\ (1)/(e^2)=0.135 \\ \\ (1)/(e^3)=0.05 \\ \\ (1)/(e^4)=0.02 \\ \\ (1)/(e^5)=0.006 \end{gathered}`

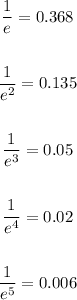
See that at t = 5α we have a small value already, then if we input p(5α) we can get

`\begin{gathered} p(5\alpha)=550(1-e^(-0.039\cdot5\alpha)) \\ \\ p(5\alpha)=550(1-0.006) \\ \\ p(5\alpha)=550(1-0.006) \\ \\ p(5\alpha)=550\cdot0.994 \\ \\ p(5\alpha)\approx547 \end{gathered}`

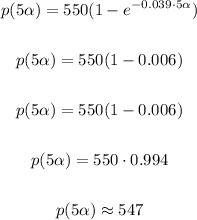
That's already very close to 550, if we want a better approximation we can use t = 8α, which will result in 549.81, which is basically 550.

Therefore, we can use t = 5α and say that 3 people are not important for our case, and say that it's basically 550, or use t = 8α and get a very close value.

In both cases, the decimal answers would be

`\begin{gathered} 5\alpha=(5)/(0.039)=128.2\text{ minutes (good approx)} \\ \\ 8\alpha=(8)/(0.039)=205.13\text{ minutes (even better approx)} \end{gathered}`