Question

Please help I need to graph this and i can only have two points

Answer 1

Given the function:

`f\mleft(x\mright)=\mleft(x+2\mright)\mleft(x-4\mright)`

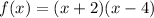
You can rewrite it as follows:

`y=\mleft(x+2\mright)\mleft(x-4\mright)`

You need to remember that the y-value is zero when the function intersects the x-axis. Then, you need to make it equal to zero, in order to find the x-intercepts:

`\begin{gathered} 0=\mleft(x+2\mright)\mleft(x-4\mright) \\ (x+2)(x-4)=0 \end{gathered}`

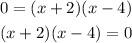
Solving for "x", you get these two values:

`\begin{gathered} x+2=0\Rightarrow x_1=-2 \\ \\ x-4=0\Rightarrow x_2=4 \end{gathered}`

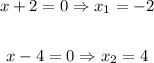
In order to find the vertex, you can follow these steps:

1. Find the x-coordinate of the vertex with this formula:

`x=-(b)/(2a)`

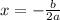
To find the value of "a" and "b", you need to multiply the binomials of the equation using the FOIL Method. This states that:

`\mleft(a+b\mright)\mleft(c+d\mright)=ac+ad+bc+bd`

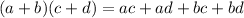
Then, in this case, you get:

`\begin{gathered} y=(x)(x)-(x)(4)+(2)(x)-(2)(4) \\ y=x^2-4x+2x-8 \end{gathered}`

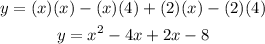
Add the like terms:

`y=x^2-2x-8`

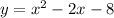
Notice that, in this case:

`\begin{gathered} a=1 \\ b=-2 \end{gathered}`

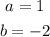
Then, you can substitute values into the formula and find the x-coordinate of the vertex of the parabola:

`x=-((-2))/(2\cdot1)=-((-2))/(2)=1`

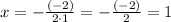
2. Substitute that value of "x" into the function and then evaluate, in order to find the y-coordinate of the vertex:

`\begin{gathered} y=x^2-2x-8 \\ y=(1)^2-2(1)-8 \\ y=1-2-8 \\ y=-9 \end{gathered}`

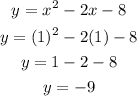
Therefore, the vertex of the parabola is:

`(1,-9)`

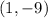
Knowing the x-intercepts and the vertex of the parabola, you can graph it.

Hence, the answer is: