Question

Calculate the total capacitance of three capacitors 30µF, 20µF & 12µF connected in parallel across a d.c supply The answer is :Consider that the equivalent capacitance of three capacitors C1, C2 and C3 in parallel is given by:C=C1+C2+C3In this case:C1 = 30µFC2 = 20µFC3 = 12µFReplace the previous values into the formula for C and simplify:C=30μF+20μF+12μF=62μFHence, the total capacitance is 62µFQuestion 5 : Calculate the total charge on the capacitors connected in parallel if the supply voltage is 500V. Sketch a circuit diagram and label this to show how the charges are located

Answer 1

The circuit diagram is shown below:

From the diagram we notice that the same voltage will flow in every capacitor, this will be helpful later.

We know that this three capacitors are equivalent to a single equivalent capacitor with 62µF capacitance. The charge in this equivalent capacitor is:

`Q_(eq)=(62*10^(-6))(500)=0.031`

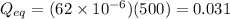
Now, as we mentioned, the voltage is the same in each capacitor then the charge in each of them is:

`\begin{gathered} Q_1=(30*10^(-6))(500)=0.015 \\ Q_2=(20*10^(-6))(500)=0.01 \\ Q_3=(12*10^(-6))(500)=0.006 \end{gathered}`

To check if this is correct we need to remember that the charge in the equivalent capacitor is equal to the sum of the charge in each capactior; for this case this conditon is fulfil; therefore we conclude that:

• The charge in the first capacitor is 0.015 C

,

• The charge in the second capacitor is 0.01 C

,

• The charge in the third capacitor is 0.006 C

The diagram with the labels is shown below: