Question

I need help on this showing step by step work

Answer 1

Notice that we have two solid shapes and we want to find the surface area of the composite.

We have a triangular prism on a cuboid.

Note: Formula For Finding the Surface Area Of A Cuboid

`Surface\text{ }Area=2(lw+lh+wh)`

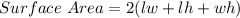
From the question, we have that

`\begin{gathered} Length(l)=12cm \\ Width(w)=4cm \\ Height(h)=14cm \end{gathered}`

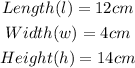
The area will be

`\begin{gathered} Surface\text{ A}rea=2(lw+lh+wh) \\ \\ Surface\text{ A}rea=2(12(4)+12(14)+4(14)) \\ \\ Surface\text{ A}rea=2(48+168+56) \\ \\ Surface\text{ A}rea=2(272) \\ \\ Surface\text{ A}rea=544cm^2 \end{gathered}`

Now, we find the Area of the Triangular Prism

Note: Formula To Use

From the question, we have

`\begin{gathered} b=4cm \\ h=2√(3)\text{ \lparen since the triangle is an equilateral triangle\rparen} \\ L=12cm \\ S_1=S_2=S_3=4cm \end{gathered}`

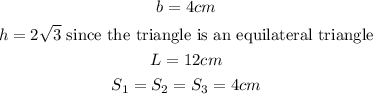
Substituting we have

`\begin{gathered} Surface\text{ }Area=bh+L(S_1+S_2+S_3) \\ \\ Surface\text{ }Area=4(2√(3))+12(4+4+4) \\ \\ Surface\text{ }Area=(8√(3)+144)cm^2 \end{gathered}`

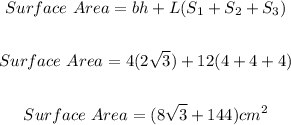
Therefore, the total surface area of the composite is

`\begin{gathered} Surface\text{ }Area=544+8√(3)+144 \\ \\ Surface\text{ }Area=(688+8√(3))cm^2 \\ or\text{ if we want to write the answer in decimal point, we have} \\ Surface\text{ }Area=701.8564065cm^2 \end{gathered}`