Question

Use the sample data and confidence level given below to complete parts (a) through (d). A drug is used to help prevent blood clots in certain patients. In clinical trials, among 4519 patients treated with the drug. 133 developed the adverse reaction of nausea Construct a 90% confidence interval for the proportion of adverse reactions. a) Find the best point estimate of the population proportion p.

Answer 1

We will have the following:

*First: We determine the standard deviation of the statistic, this is:

`\sigma=\sqrt[]{(\sum ^(133)_1(x_i-\mu)^2)/(N)}`

So, we will have:

`\mu=(\sum^(133)_1x_i)/(N)\Rightarrow\mu=(8911)/(133)\Rightarrow\mu=67`

Then:

`\sigma=\sqrt[]{(\sum^(133)_1(x_i-67)^2)/(133)}\Rightarrow\sigma=\sqrt[]{(196042)/(133)}\Rightarrow\sigma=\sqrt[]{1474}\Rightarrow\sigma=38.39270764\ldots`

And so, we obtain the standar deviation.

*Second: We determine the margin of error:

`me=cv\cdot\sigma`

Here me represents the margin of error, cv represents the critical value and this is multiplied by the standard deviation. We know that the critica value for a 90% confidence interval is of 1.645, so:

`me=1.645\cdot38.39270764\ldots\Rightarrow me=63.15600407\ldots\Rightarrow me\approx63.156`

*Third: We determine the confidence interval as follows:

`ci=ss\pm me`

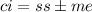
Here ci is the confidence interval, ss is the saple statistic and me is the margin of error:

`ci\approx133\pm63.156\Rightarrow ci\approx(69.844,196.256)`

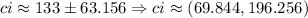
And that is the confidence interval,