Hello! First, let's remember:
We can write a point as a cartesian coordinate (x, y).
The exercise has given two points, A(4,3) and B(8,1).
a. Slope:
To calculate the slope of a line, we can use the formula below:

Let's consider A equal to the first point (4, 3) = (x1, y1), and B will be the second point (8, 1) = (x2, y2). Replacing these values in the formula:

b. Lenght of segment AB:
To find this length, we have to use another formula. Now we will calculate the distance between two points:
![\text{Distance}=\sqrt[]{(x_2-x_1)^2+(y_2_{}-y_1_{})^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/4ouuqg8ss7zhkk3ypelu.png)
Still considering A (4, 3) = (x1, y1), and B (8, 1) = (x2, y2), let's replace the values in the formula:
![\begin{gathered} \text{Distance}=\sqrt[]{(8_{}-4_{})^2+(1-3_{})^2} \\ \text{Distance}=\sqrt[]{(4_{})^2+(-2_{})^2} \\ \text{Distance}=\sqrt[]{(16^{}+4)^{}} \\ \text{Distance}=\sqrt[]{20} \\ \text{Distance}=2\sqrt[]{5} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/81sz4m4w37wx215wkq86.png)
c. Midpoint of segment AB:
This value will be the medium point. To calculate it, we'll use another formula:
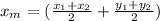
Still considering the same values for (x1, y1) and (x2, y2), let's replace them:
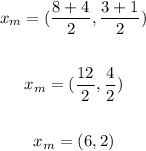
The midpoint of segment AB will be at point X (6, 2).
You can see this line represented in a cartesian plan below: