Part 3
An exponential growth function has the general form:
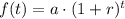
where r is the rate of growth, t is the time, and a is a constant. Notice that if calculate f(t) for t = 0, we have (1 + r)º = 1 (any number with exponent 0 equals 1). So, we obtain:
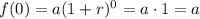
Thus, the constant a is the initial value of the function.
Now, the rate at which a bacteria grows is exponential. So, the function C(h) is given by:
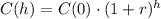
Notice that we represented the time by the letter h instead of t.
Since C(0) = 10 and C(1) = 12, we can replace h by 1 to find:
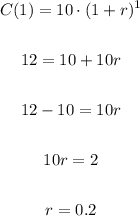
Thus, the number of cells C(h) is given by:
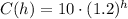
Notice that this is valid for C(15) = 154:
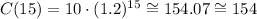
Part 1
Then, using this formula, we find:

Part 2
Now, plotting the points, rounded to the nearest whole cell, on the graph, we obtain:
Part 4
Using a calculator, we obtain the following graph of the function C(h):
Comparing the graph to the plot of the data, we see that they match.
Part 5
After a full day, it has passed 24 hours. So, we need to use h = 24 in the function C(h):
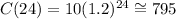
Therefore, the answer is 795 cells.