Question

A city has a population of 230,000 people. Suppose that each year the population grows by 4.25%. What will the population be after 12 years?

Answer 1

379,001.

Step-by-step explanation:

The population of the city grows by 4.25%.

This is a constant factor and models an exponential function.

An exponential population function is of the form:

`\begin{gathered} P(n)=P_0(1+r)^t \\ P_o=\text{Initial Population} \\ r\text{ = growth rate} \\ t\text{ =time in years} \end{gathered}`

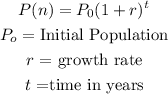
From the given problem:

`P_0=230,000,r=4.25\%=0.0425,t=12years`

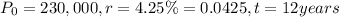
This then gives us:

`\begin{gathered} P(12)=230000(1+0.0425)^(12) \\ =230000(1.0425)^(12) \\ =379,001 \end{gathered}`

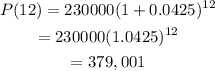
The population after 12 years will be approximately 379,001.