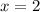Question

20. Write the slope-intercept form of the line described in the followingPerpendicular to -2+3y=-15and passing through (2, -8)

Answer 1

The equation of a line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Solve for "y" from the equation given in the exercise in order to write it in Slope-Intercept form:

`\begin{gathered} -2+3y=-15 \\ 3y=-15+2 \\ y=-(13)/(2) \end{gathered}`

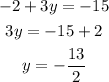
You can notice that the equation has this form:

`y=b`

Where "b" is the y-intercept.

Then, it's a horizontal line, which means that its slope is:

`m=0`

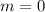
Since it is a horizontal line, the lines perpendicular to that line is a vertical line, whose slope is undefined and whose equation is:

`x=k`

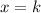
Where "k" is the x-intercept.

Knowing that the x-coordinate of any point on a vertical line is always the same, and knowing that this line passes through this point:

`\mleft(2,-8\mright)`

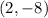
You can determine that the equation of the line is:

`x=2`