Question

? QuestionWhat is the equation of the quadratic function represented by this table?х5678910f(x)-4585-4-19HolaType the correct answer in each box. Use numerals instead of words.f(x) =(x -12 +

Answer 1

To determine the equation of the quadratic equation, which is a parabola, we substitute the coordinates of the vertex of the parabola (h,k) into the general equation.

`y=a(x-h)^2+k`

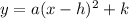
From the given, notice that the only value of f(x) that does not repeat is 8. This means that the vertex is at (7,8).

`(h,k)=(7,8)`

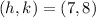
Thus, we only need to obtain the value of a.

Substitute the coordinate of a point (x,y) into the equation and the vertex as well. In this case, let us use the first given point, (5,-4).

`\begin{gathered} y=a(x-h)^2+k \\ \\ (5,-4)\rightarrow-4=a(5-7)^2+8 \end{gathered}`

Simplify the obtained equation.

`\begin{gathered} (5,-4) \\ -4=a\mleft(5-7\mright)^2+8 \\ -4=a\mleft(-2\mright)^2+8 \\ -4=a(4)+8 \\ -4-8=4a \\ -12=4a \\ a=(-12)/(4) \\ a=-3 \end{gathered}`

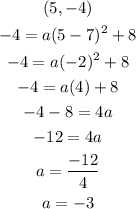
Now that we have the value of a, substitute the coordinates of the obtained vertex and the value of a into the equation of the quadratic equation.

`\begin{gathered} y=a(x-h)^2+k \\ y=-3(x-7)^2+8 \end{gathered}`

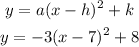
To check, the graph of the given function is as follows:

Therefore, the equation of the quadratic equation is y=-3(x-7)²+8.