Solution:
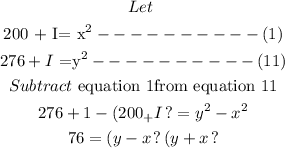
Now y+x and y-x differ in 2x.
One of them is even, because their product is even, so the other must be even too.
76=2*2*19 and 19 is prime.
We can assume x,y>=0,
Thus, y+x=2.19, and y-x=2
from here y=20, x=18
Therefore,
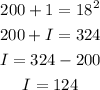
The answer is I = 124