Given that the Confidence Interval for a population mean:
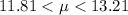
In this case, you can set up these two equations:
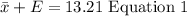
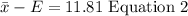
Because by definition:
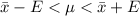
Where "ME" is the margin of error and this is the mean:
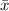
In this case, in order to find the "ME", you need to follow these steps:
1. Add Equation 1 and Equation 2:
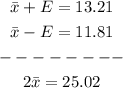
2. Solve for the mean:
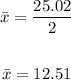
3. Substitute the mean into Equation 1 and solve for "ME":

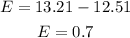
Hence, the answer is:
