Question

A tree casts a shadow 10 ft long. A boy standing next to the tree casts a shadow 2.5 ft long. The triangle shown for the tree and its shadow is similar to the triangle shown for the boy and his shadow. If the boy is 5 ft tall, how tall is the tree?

Answer 1

Boy; 5ft tall: 2.5ft shadow = 5:2.5.
Tree; x ft tall: 10ft shadow.
10 * 5 /2.5 = 20.
Tree is 20ft tall.

Answer 2

As per the statement:

Shadow of tree = 10 ft

Shadow of boy = 2.5 ft

and

height of the boy = 5 ft

we have to find the height of the tree.

Since, the given triangles are similar their corresponding sides are in proportions

then;

`\frac{\text{Shadow of tree}}{\text{Shadow of boy}} = \frac{\text{Height of tree}}{\text{Height of boy}}`

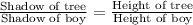
Substitute the given values;

`(10)/(2.5) = \frac{\text{Height of tree}}{5}`

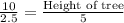
Multiply both sides by 5 we have;

`\text{Height of tree} = (10)/(2.5) * 5 = (100 \cdot 5)/(25)= 4 \cdot 5 = 20`

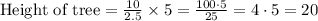
Therefore, the height of the tree is , 20 ft