Question

How many hours did the plumber work to fix the plumbing

Answer 1

The total cost of the fix is C = $375.

The plumber charges a fixed rate per call of F = $50 and charges a variable rate of v = $25 per hour, if h is the number of hours he worked, we can write:

`\begin{gathered} C=F+v\cdot h \\ 375=50+25\cdot h \end{gathered}`

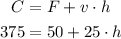
This equation shows that the total cost is equal to the fixed cost plus the variable cost. The variable cost is equal to the hourly rate times the number of hours of work.

Then, we can calculate h as:

`\begin{gathered} 375=50+25h \\ 375-50=25h \\ 325=25h \\ h=(325)/(25) \\ h=13 \end{gathered}`

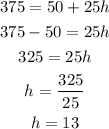
Answer: he worked 13 hours.

NOTE:

Table of values:

If we need to use a table of values to solve this, we will have two columns: one for the number of hours and the other for the total cost.

We can make the table have more detail and separate the cost column in 3: one for the fixed cost, one for the variable cost and the last one for the total cost.

Then, we would write in each column:

1) Hours: the number of hours, from 0 to the amount we consider.

2) Fixed cost: this column will have the value $50 for all the rows, as it is independent of the number of hours.

3) Variable cost: this column will have values proportional to the hours. This values will be 25 times the number of hours.

4) Total cost: this column will add both the fixed cost and variable cost.

Then, we will obtain the following table.

We can now look for the value $375 in the Total cost column.

We find that this cost correspond to 13 hours:

Graph:

We can now use the data from the table to graph the total cost in function of the number of hours.