Question

Consider the following quadratic function Part 3 of 6: Find the x-intercepts. Express it in ordered pairs.Part 4 of 6: Find the y-intercept. Express it in ordered pair.Part 5 of 6: Determine 2 points of the parabola other than the vertex and x, y intercepts.Part 6 of 6: Graph the function

Answer 1

The line of symmetry is x = -3

Step-by-step explanation:

Given a quadratic function, we know that the graph is a parabola. The general form of a parabola is:

`y=ax^2+bx+c`

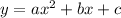
The line of symmetry coincides with the x-axis of the vertex. To find the x-coordinate of the vertex, we can use the formula:

`x_v=-(b)/(2a)`

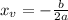
In this problem, we have:

`y=-x^2-6x-13`

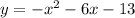
Then:

a = -1

b = -6

We write now:

`x_v=-(-6)/(2(-1))=-(-6)/(-2)=-(6)/(2)=-3`

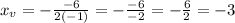Part 3:

For this part, we need to find the x-intercepts. This is, when y = 0:

`-x^2-6x-13=0`

To solve this, we can use the quadratic formula:

`x_(1,2)=(-(-6)\pm√((-6)^2-4\cdot(-1)\cdot(-13)))/(2(-1))`

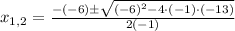
And solve:

`x_(1,2)=(6\pm√(36-52))/(-2)`
`x_(1,2)=(-6\pm√(-16))/(2)`

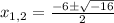
Since there is no solution to the square root of a negative number, the function does not have any x-intercept. The correct option is ZERO x-intercepts.

Part 4:

To find the y intercept, we need to find the value of y when x = 0:

`y=-0^2-6\cdot0-13=-13`

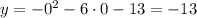
The y-intercept is at (0, -13)

Part 5:

Now we need to find two points in the parabola. Let-s evaluate the function when x = 1 and x = -1:

`x=1\Rightarrow y=-1^2-6\cdot1-13=-1-6-13=-20`
`x=-1\Rightarrow y=-(-1)^2-6\cdot(-1)-13=-1+6-13=-8`

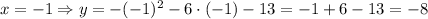
The two points are:

(1, -20)

(-1, -8)

Part 6:

Now, we can use 3 points to find the graph of the parabola.

We can locate (1, -20) and (-1, -8)

The third could be the vertex. We need to find the y-coordinate of the vertex. We know that the x-coordinate of the vertex is x = -3

Then, y-coordinate of the vertex is:

`y=-(-3)^2-6(-3)-13=-9+18-13=-4`

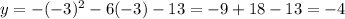
The third point we can use is (-3, -4)

Now we can locate them in the cartesian plane:

And that's enough to get the full graph: