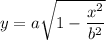Question

Solve the equation for an ellipse for y. Assume that y > 0. y^2/a^2 + x^2/b^2 = 1

Answer 1

The required value of y is:

`y=a\sqrt{1-(x^2)/(b^2)}`

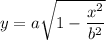
Explanation:

We have to solve the equation for an ellipse for y.

That means we have to find the value of y in terms of x from the given equation.

The equation of an ellipse is given as:

`(y^2)/(a^2)+(x^2)/(b^2)=1`

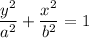
We will multiply both side by
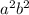`a^2b^2` to obtain:

`b^2y^2+a^2x^2=a^2b^2`

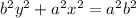
Now we will take the term of variable 'x' to the right hand side to obtain:

`b^2y^2=a^2b^2-a^2x^2\\\\y^2=(a^2b^2-a^2x^2)/(b^2)\\\\y^2=(a^2b^2)/(b^2)-(a^2x^2)/(b^2)\\\\y^2=a^2-(a^2x^2)/(b^2)\\\\y^2=a^2(1-(x^2)/(b^2))`

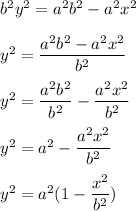
No on taking square root on both the side we obtain:

`y=a\sqrt{1-(x^2)/(b^2)}`

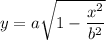
Hence, the required value of y is:

`y=a\sqrt{1-(x^2)/(b^2)}`

Answer 2

multiply each term by a^2b^2:-

b^2y^2 + a^2x^2 = a^2b^2
subtract a^2x^2 from both sides
b^2y^2 = a^2b^2 - a^2x^2
Now divide both sides by b^2

y^2 = a^2 - a^2x^2 / b^2 = a^2 (1 - x^2/b^2)

take positive square root ( because y > 0)

y = a sqrt(1 - x^2/b^2)