1 Answer

Ask a Question

David Grenier · Answer 1 · 2023-09-24T20:30:55+0000

Since the triangle is equilateral, all of its interior angles have a measure of 60º.

Substract the area of the triangle from the area of a circular sector with radius 7cm enclosed by an angle of 60º to find the area of the shaded region.

The area of an equilateral triangle with side length L is:

$A=\frac{\sqrt[]{3}}{4}L^2$

The area of a circular sector of radius r enclosed by an angle of θ degrees is:

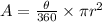
$A=(\theta)/(360)*\pi r^2$

Replace θ=60 and r=7cm to find the area of the circular sector:

$A_c=(60)/(360)*3.14*(7\operatorname{cm})^2=25.643\ldots cm^2$

Replace L=7cm to find the area of the triangle:

$A_T=\frac{\sqrt[]{3}}{4}*(7\operatorname{cm})^2=21.2176\ldots cm^2$

Then, the area of the shaded region is:

$\begin{gathered} A_C-A_T=25.6433\ldots cm^2-21.2176\ldots cm^2 \\ =4.4257\ldots cm^2 \\ \approx4.43\operatorname{cm}^2 \end{gathered}$

Therefore, the area of the shaded region to 3 significant figures, is:

$4.43\operatorname{cm}^2$

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions