Question

What is partial derivative of z=(2x+3y)^10 with respect to x,y?

Answer 1

Not sure if you mean to ask for the first order partial derivatives, one wrt x and the other wrt y, or the second order partial derivative, first wrt x then wrt y. I'll assume the former.


`\frac\partial{\partial x}(2x+3y)^(10)=10(2x+3y)^9*2=20(2x+3y)^9`


`\frac\partial{\partial y}(2x+3y)^(10)=10(2x+3y)^9*3=30(2x+3y)^9`

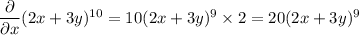
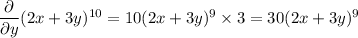
Or, if you actually did want the second order derivative,


`(\partial^2)/(\partial y\partial x)(2x+3y)^(10)=\frac\partial{\partial y}\left[20(2x+3y)^9\right]=180(2x+3y)^8*3=540(2x+3y)^8`

and in case you meant the other way around, no need to compute that, as
`z_(xy)=z_(yx)` by Schwarz' theorem (the partial derivatives are guaranteed to be continuous because
`z` is a polynomial).

Answer 2

Explanation:

Given that z is a function of x,y

`z=(2x+3y)^(10)`

Partially differentiate wrt x and y separately to get

`\frac\partial{\partial x}(2x+3y)^(10)=10(2x+3y)^9*2=20(2x+3y)^9\\\frac\partial{\partial y}(2x+3y)^(10)=10(2x+3y)^9*3=30(2x+3y)^9`