Question

identify whether the series infinity sigma i=1 8(5/6)^i-1 is a convergent or divergent geometric series and find the sum if possible

Answer 1

The sum is convergent. I'll assume the 8 isn't an attempt at using the infinity symbol, so that you have


`\displaystyle\sum_(i=1)^\infty 8\left(\frac56\right)^(i-1)`

This converges because the common ratio between terms is smaller than 1.

The sum is


`\frac8{1-\frac56}=48`

since


`\displaystyle\sum_(i=1)^\infty ar^(i-1)=a\lim_(n\to\infty)\sum_(i=1)^nr^(i-1)=a\lim_(n\to\infty)(1-r^n)/(1-r)=\frac a{1-r}`

if
`|r|<1`.

Answer 2

The sum of infinite geometric series is:

40

Explanation:

We have to find the sum of the geometric series which is given as:

`\sum^(\infty)_(i=1) 8* ((5)/(6))^i`

which could also be written as:

`8\sum^(\infty)_(i=1) ((5)/(6))^i`

As we know that any infinite series of the form:

`\sum^(\infty)_(i=1)x^i`

is convergent if |x|<1

Here we have:

x=5/6<1

Hence,the infinite series is convergent.

Also we know that for infinite geometric series the sum is given as:

`S=(a)/(1-r)`

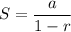
Here we have:

a=5/6 and common ration r=5/6

Hence, the sum of series is:

`8\sum^(\infty)_(i=1) ((5)/(6))^i=8* (((5)/(6))/(1-(5)/(6)))\\\\=8* (((5)/(6))/((1)/(6)))\\\\=8* 5\\\\=40`

Hence, the sum of series is:

40