Question

Choose the algebraic description that maps ΔABC onto ΔA′B′C′ in the given figure.Question 7 options:A) (x, y) → (x + 4, y + 8)B) (x, y) → (x + 8, y + 4)C) (x, y) → (x – 4, y – 8)D) (x, y) → (x + – 8, y – 4)

Answer 1

Step 1

Given the triangle, ABC translated to A'B'C'

Required to find the algebraic description that maps triangle ABC and A'B'C'

Step 2

The coordinates of points A, B,C are in the form ( x,y)

Hence

`\begin{gathered} A\text{ has a coordinate of ( -3,-2)} \\ B\text{ has a coordinate of (-6,-5)} \\ C\text{ has a coordinate of (-1,-4)} \end{gathered}`

Step 3

Find the algebraic description that maps triangle ABS TO A'B'C'

`\begin{gathered} A^(\prime)\text{ has a coordinate of (5,2)} \\ B^(\prime)\text{ has a coordinate of ( 2,-1)} \\ C^(\prime)\text{ has a coordinate of ( 7, 0)} \end{gathered}`

The algebraic description is found using the following;

`\begin{gathered} (A^(\prime)-A^{})=(x^(\prime)-x,\text{ y'-y)} \\ OR \\ (B^(\prime)-B)=(x^(\prime)-x,\text{ y'-y)} \\ OR \\ (C^(\prime)-C)=(x^(\prime)-x,\text{ y'-y)} \end{gathered}`

Hence,

`\begin{gathered} =\text{ ( 5-(-3)), (2-(-2))} \\ =(8,4) \\ \text{Hence the algebraic description from triangle ABC to A'B'C' will be } \\ =(x,y)\Rightarrow(x\text{ + 8, y+4)} \end{gathered}`

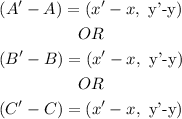
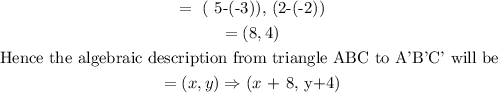
Hence the answer is option B