Question

Are f(x) and g(x) inverse functions across the domain (5, + infinity)

Answer 1

Given:

`\begin{gathered} F(x)=√(x-5)+4 \\ G(x)=(x-4)^2+5 \end{gathered}`

Required:

Find F(x) and G(x) are inverse functions or not.

Step-by-step explanation:

Given that

`\begin{gathered} F(x)=√(x-5)+4 \\ G(x)=(x-4)^(2)+5 \end{gathered}`

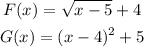
Let

`F(x)=y`
`\begin{gathered} y=√(x-5)+4 \\ y-4=√(x-5) \end{gathered}`

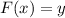
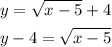
Take the square on both sides.

`(y-4)^2=x-5`

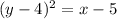
Interchange x and y as:

`\begin{gathered} (x-4)^2=y-5 \\ y=(x-4)^2+5 \end{gathered}`

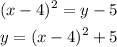
Substitute y = G(x)

`G(x)=(x-4)^2+5`

This is the G(x) function.

So F(x) and G(x) are inverse functions.

`\begin{gathered} G(x)-5=(x-4)^2 \\ √(G(x)-5)=x-4 \\ x=√(G(x)-5)+4 \end{gathered}`

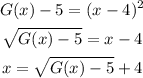
Final Answer:

Option A is the correct answer.