ANSWER:
(a)
(b)
Explanation:
(a)
We must do the following transformation:
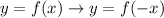
In this case, reflects f(x) about the y-axis. The rule that follows the above, is like this:
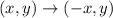
We apply the rule to the points of the function and it would be:
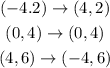
We graph and we have:
(b)
We must do the following transformation:

In this case, reflects f(x) about the x-axis. The rule that follows the above, is like this:
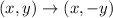
We apply the rule to the points of the function and it would be:
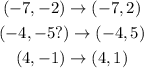
We graph and we have: