We are going to use Binomial Probability Distribution
Probability that they have no landline = q = 27/100 = 0.27
Probability that they have landline = p = 1 - 0.27 = 0.73
Now, to find the probability that at least one of them does not have a landline, we have to find the probability that all the five have a landline first.
So let's find the probability that all the five have a landline:
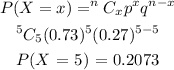
So the probability that all the five have a landline = 20.73%
Now is the time to find the probability that at least one of them does not have a landline:
P(at least one has no landline) = 1 - P(All have landline)
= 1 - 0.2073
= 0.7927
So the probability that at least one of them does not have a landline = 79.27%
That's all Please