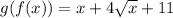Question

Use the pair of functions to find f(g(x)) and g(f(x)). Simplify your answers.f(x)=sqrt(x)+2g(x)=x^2+7f(g(x))= ?g(f(x))= ?

Answer 1

`\begin{gathered} \begin{equation*} f(g(x))=√(x^2+7)+2 \end{equation*} \\ \begin{equation*} g(f(x))=x+4√(x)+11 \end{equation*} \end{gathered}`

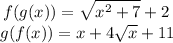
Explanation:

Given the functions f(x) and g(x) below:

`\begin{gathered} f(x)=√(x)+2 \\ g\mleft(x\mright)=x^2+7 \end{gathered}`

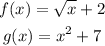
Part A

We want to find the simplified form of f(g(x)).

`f(x)=√(x)+2`

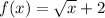
Replace x with g(x):

`f(g(x))=√(g(x))+2`

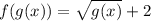
Finally, enter the expression for g(x) and simplify if possible:

`\implies f\mleft(g\mleft(x\mright)\mright)=√(x^2+7)+2`

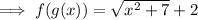
Part B

We want to find the simplified form of g(f(x)). To do this, begin with g(x):

`g\mleft(x\mright)=x^2+7`

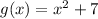
Replace x with f(x):

`g(f(x))=[f(x)]^2+7`

Finally, enter the expression for f(x) and simplify if possible:

`\begin{gathered} g\mleft(f\mleft(x\mright)\mright)=(√(x)+2)^2+7 \\ =(√(x)+2)(√(x)+2)+7 \\ =x+2√(x)+2√(x)+4+7 \\ \implies g(f(x))=x+4√(x)+11 \end{gathered}`

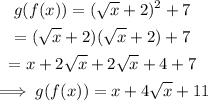
Therefore:

`\begin{equation*} g(f(x))=x+4√(x)+11 \end{equation*}`