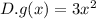Question

The functions f(x) and g(x) are shown on the graph.f(x)=x^2What is g(x)?A. g(x)=(x+3)^2B. g(x)=(x-3)^2C. g(x)=(1/3x)^2D. g(x)=3x^2

Answer 1

Given:

`f(x)=x^2`

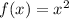
Let's find g(x).

From the given graph, we can see the graph of g(x) is compressed horizontally from f(x).

Thus, to find g(x) aply the transformation rules for function.

We have:

Horizontal compression of b units ==> f(bx)

Given the point on g(x):

(x, y) ==> (2, 12)

Let's solve for the value of the compressed factor.

We have:

`\begin{gathered} 12=b(2)^2 \\ \\ 12=b4 \\ \\ \text{Divide both sides by 4:} \\ (12)/(4)=(b4)/(4) \\ \\ 3=b \\ \\ b=3 \end{gathered}`

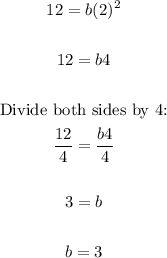
This means the graph of f(x) was compressed horizontally by a factor of 3 to get g(x).

Thus, to write the function for g(x), we have:

`g(x)=3x^2`

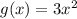
ANSWER:

`D\text{.}g(x)=3x^2`