Question

John is planning to take out a personal loan for $4,500 to buy a car. He would like to keep his monthly payments at or below $150.00 and pay the loan off in three years. Which of the following is the greatest interest rate John can accept and still meet his criteria?

a. 10.75% compounded monthly
b. 11.50% compounded monthly
c. 12.25% compounded monthly
d. 13.00% compounded monthly

Answer 1

. 12.25% compounded monthly

Answer 2

Answer: C. 12.25% compounded monthly

Explanation:

Since, the monthly payment formula for a loan is,

`P = ((PV)r)/(1-(1+r)^(-n))`

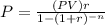
Where PV is the principal value of the loan,

r is the rate per month,

n is the number of months,

Here, PV = $ 4,500, n = 36,

Let r be the annual rate of interest,

P ≤ 150

⇒
`((4500)(r)/(12))/(1-(1+(r)/(12))^(-36))\leq 150`

⇒
`375 r \leq 150-150(1+(r)/(12))^(-36)`

⇒
`r\leq 0.1225`

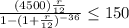
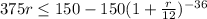
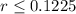
Thus, the greatest annual interest rate = 0.1225 = 12.25 %

⇒ Option C is correct.