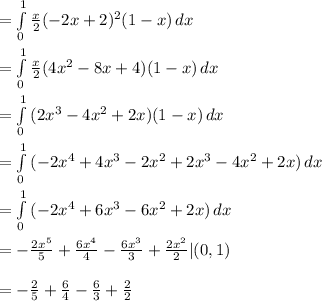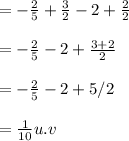Question

Evaluate the triple integrals below where E is the solid tetrahedron with vertices (0,0,0), (1,0,0), (0,2,0) and (0,0,3). I need help with finding the boundries using the graph and then solving it.

Answer 1

Hi, We can to calculate the vectors.

And the determinant will be the plan Z

Let A = (0,03), B =(0,2,0) , C = (1,0,0) and D = (0,0,0)

Then,

AB = B - A

Replacing the points:

AB = (0,2,0) - (0,0,3)

AB = (0i, 2j , -3k)
----------------------------

Already the vector AC = C -A

That's is,

AC = (1,0,0) - (0,0,3)

AC = (1i, 0j, -3k)

Then,

The plan =
`\left[\begin{array}{ccc}x&y&z\\0&2&-3\\1&0&-3\end{array}\right]`

Solving it, we will have:

Plan: -6x -3y -2z + d = 0

Replacinng any point to find the value of d

Example the point A =(0,0,3)

-6(0) -3(0) -2(3) + d = 0

-6+d = 0

d = 6

Then, The us equation will stay of form following :

-6x -3y -2z +6 = 0

or

6x + 3y +2z -6 = 0

Isolating 2z:

2z = 6 -6x - 3y

Dividing both the sides od equation by 2

z = 3 - 3x - 3y/2

Then,


`0 \leq Z \leq 3-3x- (3y)/(2)`

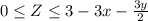
Now, Let's find the domain in xy

|y
| (0,2)
|\
| \
| \
| \ (1,0)
------------------------- x


b = Cut in y

then b will be = 2

As y = ax + b

y = ax + 2

We have the point = (1,0)

Replace in the equation

0 = a(1) + 2

0 = a + 2

Isolate a

a = -2

Then us stay:

y = -2x + 2



`0 \leq y \leq -2x+2`

-------------------------------------

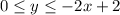
With ,



`0 \leq x \leq 1`

----------------------------------------



`\\ \int\limits^1_0 {} \, \int\limits^ \frac{-2x+2}{} _0 {} \, \int\limits^ \frac{3-3x- (3y)/(2) }{} _0 {(xy)} \, dzdydx \\ \\ =\int\limits^1_0 {} \, \int\limits^ \frac{-2x+2}{} _0 {} \,(3xy -3x^2y - (3xy^2)/(2) )dydx \\ \\ =\int\limits^1_0 {} \, ( (3xy^2)/(2) - (3x^2y^2)/(2) - (3xy^3)/(6) )|0,(-2x+2)dx \\ \\ = \int\limits^1_0 {((3x(-2x+2)^2)/(2) - (3x^2(-2x+2)^2)/(2) - (3x(-2x+2)^3)/(6) )} \, dx`

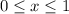
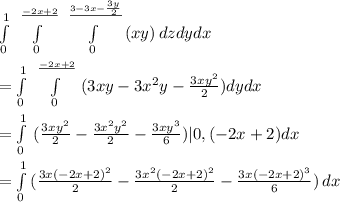
Now putting 3x/2(-2x+2)² as commu factor


`\\ = \int\limits^1_0 {((3x(-2x+2)^2)/(2) - (3x^2(-2x+2)^2)/(2) - (3x(-2x+2)^3)/(6) )} \, dx \\ \\ = \int\limits^1_0 { (3x)/(2)(-2x+2)^2[ 1- x- (1)/(3) (-2x+2)] } \, dx \\ \\ = \int\limits^1_0 { (3x)/(2)(-2x+2)^2[ 1- x+ (2x)/(3) - (2)/(3) ] } \, dx \\ \\ = \int\limits^1_0 { (3x)/(2)(-2x+2)^2[ (1)/(3) - (x)/(3)] } \, dx \\ \\ = \int\limits^1_0 { (3x)/(2)(-2x+2)^2( (1-x)/(3) ) } \, dx`


`\\ = \int\limits^1_0 { (x)/(2)(-2x+2)^2(1-x) } \, dx \\ \\ = \int\limits^1_0 { (x)/(2)(4x^2-8x+4)(1-x) } \, dx \\ \\ = \int\limits^1_0 {(2x^3-4x^2+2x) (1-x) } \, dx \\ \\ = \int\limits^1_0 {(-2x^4+4x^3-2x^2+2x^3-4x^2+2x)} \, dx \\ \\ = \int\limits^1_0 {(-2x^4+6x^3-6x^2+2x)} \, dx \\ \\ = -(2x^5)/(5) + (6x^4)/(4) - (6x^3)/(3) + (2x^2)/(2) |(0,1) \\ \\ = -(2)/(5) + (6)/(4) - (6)/(3) + (2)/(2)`


`\\ =-(2)/(5) + (3)/(2) - 2 + (2)/(2) \\ \\ = -(2)/(5) -2+ (3+2)/(2) \\ \\ = -(2)/(5) -2 + 5/2 \\ \\ = (1)/(10) u.v`