Question

Compute the sums below. (Assume that the terms in the first sum are consecutive terms of an arithmetic sequence.) 9 + 4 + (-1) + ... + (-536)

Answer 1

The terms below make an A.P. Now we are told to find the sum of the AP.

Sum of an AP is given by

`S\text{ = }(n)/(2)\lbrack2a\text{ + (n-1)d\rbrack}`

Where S = sum of the AP, a = first term = 9, d = -5, n= ?

So we have to find n first before we can find the sum. The nth term which is the last term = -536. So we will use it to find the number of terms "n"

`\begin{gathered} \text{From T}_{n\text{ }}=\text{ a +(n-1)d where T}_{n\text{ }}=\text{ -536} \\ -536\text{ = 9+(n-1)-5} \\ -536\text{ = 9-5n+5} \\ -536\text{ = 14-5n} \\ -5n\text{ = -536-14} \\ -5n\text{ = -550} \\ n\text{ = 110} \end{gathered}`

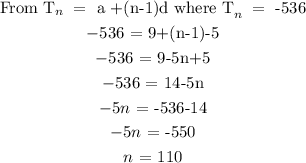
Now let's find the sum

`\begin{gathered} S\text{ = }(n)/(2)\lbrack2a\text{ + (n-1)d\rbrack} \\ S\text{ = }(110)/(2)\lbrack2*9\text{ + (110-1)-5\rbrack} \\ S\text{ = 55\lbrack{}18+(119)-5\rbrack} \\ S\text{ = 55\lbrack{}18 - 595\rbrack} \\ S\text{ = 55}*-577 \\ S\text{ = -31735} \end{gathered}`

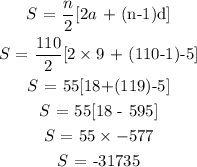
Therefore, the sum = -31735