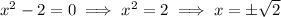First, pull out a factor of

.
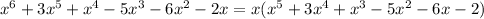
Notice that when

(which you can arrive at via the rational root theorem), you have
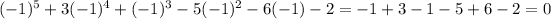
which means you can pull out a factor of
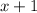
. Upon dividing you get
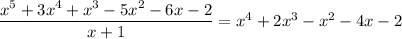
The rational root theorem will come in handy again, suggesting that

appears a second time as a root, which means
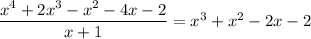
Now this is more readily factored without having to resort to the rational root theorem. You have
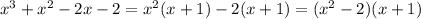
so in fact,

shows up as a root for a third time.
So, you have

Two roots are obvious,

and

(with multiplicity 3). The remaining two are given by