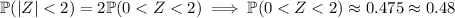Since

is 2 standard deviations above the mean, you're looking for the probability that
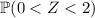
The empirical rule says that approximately 95% of a normal distribution lies within 2 standard deviations of the mean, or
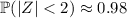
.
Since the normal distribution is symmetric, you have