Question

If the circumference of the circular base of a cylinder is doubled, how does the volume of the cylinder change?

Question 16 options:

The volume is quadrupled.


The volume is tripled.


The volume is eight times larger.


The volume is doubled.

Answer 1

V=hpir^2

C=2pir
when it is doubled
newC=2pi(2r)
that means radius is doubled

sub 2r for r in volume

V=hpi(2r)^2
v=hpi4r^2
v=4(hpir^2)
it is quadrupled


answer is 1st option

Answer 2

The volume is quadrupled

Explanation:

we know that

The volume of the cylinder is equal to

`V=\pi r^(2) h`

In this problem

If the circumference of the circular base is doubled then , the radius is doubled too, because the circumference and the radius represent a linear direct variation

therefore

The new volume is equal to

`V=\pi (2r)^(2) h`

`V=4\pi r^(2) h`

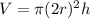
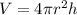
The new volume is four times the original volume