Question

(08.01)Consider the following pair of equations: −x − y = −5 y = x + 1 If the two equations are graphed, at what point do the lines representing the two equations intersect?

Answer 1

The equations will intersect at the solution of the equations.
A) −x − y = −5
B) y = x + 1 OR

B) -x + y = + 1
Adding equations A and B
-2x = -4
x = 2

Substituting x =2 into EquationB

-2 + y = + 1
y = 3

Answer 2

Answer: The required point of intersection of the lines is (2, 3).

Step-by-step explanation: The given system of linear equations is as follows:

`-x-y=-5~~~~~~~~~~~~~~~~~~~(i)\\\\y=x+1~~~~~~~~~~~~~~~~~~~~~~~(ii)`

We are to find the point of intersection of the two lines if they are graphed.

To do this, we need to solve the pair of equations and the solution will be the required point of intersection of the lines when graphed.

Now,

Substituting the value of 'y' from equation (ii) in equation (i), we have

`-x-y=-5\\\\\Rightarrow -x-(x+1)=-5\\\\\Rightarrow -2x-1=-5\\\\\Rightarrow -2x=-4\\\\\Rightarrow x=2,`

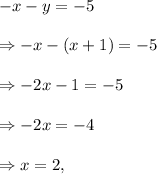
and from equation (ii), we get

`y=x+1=2+1=3.`

So, the solution of the pair of equations is (x, y) = (2, 3), and thus (2, 3) is the required point of intersection of the lines when graphed.

To verify, we have drawn the graphs of equations (i) and (ii) in the attached file.

We can see that the point of intersection is (2, 3). Hence verified.