Question

I have a question about how to solve graphing a system of inequalities and about how to do the (0,0)

Answer 1

The given system of inequality is

`\begin{gathered} 2x-3y>-12 \\ x+y\ge-2 \end{gathered}`

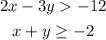
At first, we must draw the lines to represent these inequalities

`2x-3y=-12`

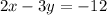
Let x = 0, then find y

`\begin{gathered} 2(0)-3(y)=-12 \\ 0-3y=-12 \\ -3y=-12 \\ (-3y)/(-3)=(-12)/(-3) \\ y=4 \end{gathered}`

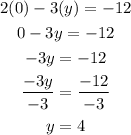
The first point is (0, 4)

Let y = 0

`\begin{gathered} 2x-3(0)=-12 \\ 2x-0=-12 \\ 2x=-12 \\ (2x)/(2)=(-12)/(2) \\ x=-6 \end{gathered}`

The second point is (-6, 0)

We will do the same with the second line

Let x = 0

`\begin{gathered} 0+y=-2 \\ y=-2 \end{gathered}`

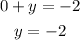
The first point is (0, -2)

Let y = 0

`\begin{gathered} x+0=-2 \\ x=-2 \end{gathered}`

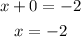
The second point is (-2, 0)

Since the sign of the first inequality is >, then the line will be dashed

Since the sign of the second inequality is >=, then the line will be solid

Let us substitute x, y by the origin point (0,0) in both inequalities to find the shaded part of each one

`\begin{gathered} 2(0)-3(0)>-12 \\ 0-0>-12 \\ 0>-12 \end{gathered}`

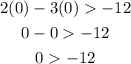
Since the inequality is true then the point (0, 0) lies on the shaded area

`\begin{gathered} 0+0\ge-2 \\ 0\ge-2 \end{gathered}`

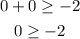
Since the inequality is true, then point (0, 0) lies in the shaded area

Let us draw the graph

The red line represents the first inequality

The blue line represents the second inequality

The area of two colors is the area of the solution

Point (0, 0) lies in this area, then it is a solution for the given system of inequalities