In order to calculate the number of permutations, first we start with the factorial of the number of letters.
There are 10 letters, so we start with the factorial of 10.
Then, we need to check the number of repetitions. Each repetition will be a factorial in the denominator:
![x=\frac{10!}{a!\cdot b!\operatorname{\cdot}...}]()
We have four repetitions of aa, two repetitions of bb, two repetitions of cc and two repetitions of RR, therefore the final expression for the number of permutations is:
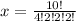
Calculating this expression, we have:
![x=\frac{10\operatorname{\cdot}9\operatorname{\cdot}8\operatorname{\cdot}7\operatorname{\cdot}6\operatorname{\cdot}5\operatorname{\cdot}4!}{4!\operatorname{\cdot}2\operatorname{\cdot}2\operatorname{\cdot}2}=\frac{10\operatorname{\cdot}9\operatorname{\cdot}8\operatorname{\cdot}7\operatorname{\cdot}6\operatorname{\cdot}5}{8}=18900]()
Therefore there are 18900 permutations.