Question

Graph A) -f(x) B) f(x+2) -4Then find the domain and range of each

Answer 1

a. Graph -f(x):

By the transformations rules for functions, the graph of -f(x) is equal to a reflection over the x-axis, and a change of the y-coordinates:

`(x,y)\rightarrow(x,-y)`

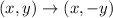
Then, given the function:

`f(x)=\sqrt[]{x}`

The graph of -f(x) is:is

The domain of the function is the set of all possible x-values, then it is:

`\lbrack0,+\infty)`

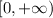
The range is the set of all possible values of the function, then it is:

`\lbrack0,-\infty)`

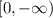
b. Graph f(x+2)-4:

The transformation f(x+2) is an horizontal translation left 2 units.

And the transformation f(x+2)-4 is a vertical translation down 4 units.

Then, the coordinates of this graph in comparison to the given graph are:

`(x,y)\rightarrow(x-2,y-4)`

Then for the point (1,1) the new coordinates are (1-2,1-4)=(-1,-3).

For (4,2): the new coordinates (4-2,2-4)=(2,-2)

For (9,3): the new coordinates (9-2,3-4)=(7,-1)

The graph is:

The domain of this function is:

`\lbrack-2,+\infty)`

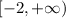
And the range is:

`\lbrack-4,+\infty)`