Question

Given that sin(0)= 10/ 13 and 0 is in Quadrant II, what is cos(20)? Give an exact answer in the form of a fraction. ,

Answer 1

Given the image in the question tab, the following are the solution steps to the answer

Step 1: Write out the function

`\begin{gathered} \sin \theta=(10)/(13) \\ \text{since }\sin \theta=(opp)/(hyp) \\ \therefore opp=10,\text{ hyp=13} \end{gathered}`

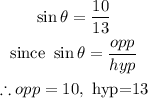
Step 2: Solve for the adjacent using the pythagoras theorem

`\begin{gathered} \text{hyp}^2=opp^2+adj^2 \\ 13^2=10^2+adj^2 \\ \text{adj}^2=13^2-10^2 \\ \text{adj}=\sqrt[]{169-100} \\ \text{adj}=\sqrt[]{69} \end{gathered}`

Step 3: Calculate the value of cos2Ф

`\begin{gathered} cos2\theta=\cos ^2\theta-\sin ^2\theta \\ \cos 2\theta=(\frac{\text{adj}}{\text{hyp}})^2-((opp)/(hyp))^2 \\ \cos 2\theta=(\frac{\sqrt[]{69}}{13})^2-((10)/(13))^2 \\ \cos 2\theta=(69)/(169)-(100)/(169) \\ \cos 2\theta=-(31)/(169) \end{gathered}`

Hence, the value of cos2Ф is -31/169.