Question

Find all solutions of the equation sin^2 x=2sinx+3

The answer is A+Bkpi where k is any integer and 0 A=?. B=?

Answer 1

`\sin^2x=2\sin x+3`

`\sin^2x-2\sin x-3=0`

`(\sin x-3)(\sin x+1)=0`

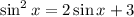
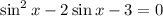
which means either
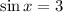
`\sin x=3` or
`\sin x=-1`. The equation has no solution, since
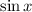
`\sin x` is always bounded between -1 and 1. The second has one solution at
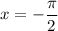
`x=-\frac\pi2`, and any number of complete revolutions will also satisfy this equation, so in general the solution would be
`-\frac\pi2+2k\pi` where
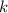
`k` is any integer.

So you could choose
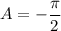
`A=-\frac\pi2` and
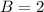
`B=2`.