Question

Jeff tosses a can of soda pop to Karen, who is standing on her 3rd floor balcony a distance of 8.5m above Jeff’s hand. Jeff gives the can an initial velocity of 16m/s, fast enough so that the can goes up past Karen, who catches the can on its way down. Calculate the velocity of the can the instant before Karen grabs the can. How long after Jeff tosses the can does Karen have to prepare to catch it?

Answer 1

9.51 m/s

Step-by-step explanation

We know that Jeff is 8.5m below Karen. He tosses the can up with initial velocity u = 16m/s and it passes where Karen is, so the maximum height of the can is 8.5m plus some more meters x. Then Karen catches the can in its way down, so when she does the can goes this distance x.

Let's find this distance. The height of an object thrown up with initial velocity u is:

`y=ut-(1)/(2)gt^2`

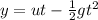
We know u = 16m/s but we don't know the time. This we can find from the final velocity of the can:

`v=u-gt`

At its maximum height the velocity is zero:

`0=u-gt`

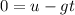
Solving for t:

`t=(u)/(g)`

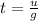
If we assume g = 9.8m/s²:

`t=(16m/s)/(9.8m/s^2)=1.63s`

We know that the can was in the air for 1.63 seconds until it reached its maximum height. The maximum height is:

`y=16m/s\cdot1.63s-(1)/(2)\cdot9.8m/s^2\cdot1.63^2s^2`
`y=26.08m-13.02m=13.06m`

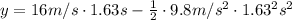
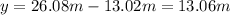
This is the maximum height of the can. The extra distance the can travelled above Karen is:

`x=13.06m-8.5m=4.56m`

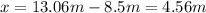
In the can's way down, the initial velocity is 0, because it starts falling after stopping in its way up. The acceleration is still the acceleration of gravity and the height it falls is x. We can find the time it took to reach Karen's hand after it started falling:

`y=(1)/(2)gt^2`

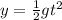
Note that in this case we use the acceleration of gravity positive because it is in the same direction of the can's motion. Solving for t:

`t=\sqrt[]{(2y)/(g)}`
`t=\sqrt[]{(2\cdot4.56m)/(9.8m/s^2)}=\sqrt[]{0.93s^2}=0.97s`

Knowing that the can was in the air for another 0.97 seconds after starting falling until it reached Karen's hand, we can find its velocity at that instant:

`v=u+gt`

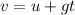
Remember that in this case u = 0:

`v=gt=9.8m/s^2\cdot0.97s=9.51m/s`

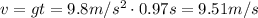
The velocity of the can the instant before Karen grabs it is 9.51 m/s