Given the equation:
![\sqrt[]{x}+1=x-\sqrt[]{x}-1](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ptchgevkxd36r65umxx3.png)
Solving for x:
![\begin{gathered} \sqrt[]{x}+\sqrt[]{x}=x-1-1 \\ 2\sqrt[]{x}=x-2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vhg8gh7onrzlrgunw31s.png)
Now, we take the square on both sides of the equation:
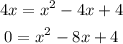
Now, using the general solution of quadratic equations:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
From the problem, we identify:
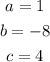
Then, the solutions are:
![\begin{gathered} x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4\cdot1\cdot4}}{2\cdot1}=\frac{8\pm\sqrt[]{64-16}}{2} \\ x=\frac{8\pm4\sqrt[]{3}}{2}=4\pm2\sqrt[]{3} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jwskk4hh5td7eulf1hi7.png)
But the original equation √(x), so x can not be negative if we want a real equation. Then, the only real solution of the equation is:
![x=4+2\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vaajtxl2fznpxogs74en.png)