Question

I just need help finding the area of shape c.

Answer 1

We need to find the area of Shape C.

Please have a look at the diagram below:

To find x, we can use the Pythagorean Theorem on the right triangle.

`\begin{gathered} 100^2+x^2=107^2 \\ \end{gathered}`

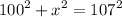
Now, let's solve for x. The steps are shown below:

`\begin{gathered} 100^2+x^2=107^2 \\ x^2=107^2-100^2 \\ x^2=11449-10000 \\ x^2=1449 \\ x=\sqrt[]{1449} \\ x=38.07 \end{gathered}`

So, the top part (dotted line) is

`\begin{gathered} x+100+x \\ =38.07+100+38.07 \\ =176.14 \end{gathered}`

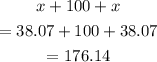
Now, we have a trapezoid. Let's find the area of the trapezoid:

`\begin{gathered} A=(1)/(2)(b_1+b_2)h \\ A=(1)/(2)(100+176.14)(100) \\ A=13,807 \end{gathered}`

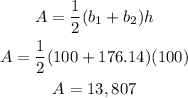
Now, we need to subtract the area labeled (K) from the area of the trapezoid found.

--------------------------------------------------------------------------------

Area k is a triangle with side lengths 117, 117, and 176.14. Let's find the area of the triangle. The diagram is shown below:

Now, we will find h, the height of the triangle using Pythagorean Theorem.

`\begin{gathered} 88.07^2+h^2=117^2 \\ h^2=117^2-88.07^2 \\ h^2=5932.6751 \\ h=\sqrt[]{5932.6751} \\ h=77.02 \end{gathered}`

The area of the triangle (region K) is,

`\begin{gathered} A=(1)/(2)bh \\ A=(1)/(2)(176.14)(77.02) \\ A=6783.15 \end{gathered}`

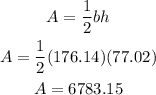
The area of region C is the area of trapezoid - area of region k (triangle). So, the area is >>>>

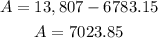
`\begin{gathered} A=13,807-6783.15 \\ A=7023.85 \end{gathered}`Answer7023.85