Question

A cubic equation has zeros at -2, 1, and 3 a) Write an eqn for a polynomial function that meets the given conditions.b) Draw the graph of a polynomial function that meets the given conditions.

Answer 1

we know that

A cubic equation has zeros at -2, 1, and 3

so

the factors of the cubic equation are

(x+2), (x-1) and (x-3)

Part a

The equation of a polynomial is

`P(x)=(x+2)\cdot(x-1)\cdot(x-3)`

Applying distributive property

`\begin{gathered} P(x)=(x^2-x+2x-2)\cdot(x-3) \\ P(x)=(x^2+x-2)\cdot(x-3) \end{gathered}`

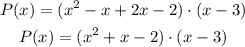
Applying distributive property again

`P(x)=x^3-3x^2+x^2-3x-2x+6`

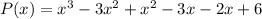
Combine like terms

`P(x)=x^3-2x^2^{}-5x+6`

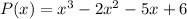
Part b

using a graphing tool

see the attached figure below