Question

 A motorboat, moving at a speed of 10 km/hour, left a pier traveling against the current of the river. Forty-five minutes after the boat left the pier, the motor of the boat broke, and the boat began drifting with the current. After three hours of drifting with the current, the boat was back at the pier where it had started. What is the speed of the current of the river?

Answer 1

so... the motorboat went up the river, at a rate of 10km/hr
against the river current, let's say... the river has a current rate,
of "r", so the boat, once we subtract "r" from 10, the boat
wasn't really going 10km per hr, it was going slower, because
the river was slowing it down, so the motorboat rate was 10-r
it went up some distance, say "d", for 45 mins
broke down
backslid for 3hrs, back to port

notice, it went up for 45mins, distance "d"
broke down, then backslid back to quarters
ahemm..... the distance it backslid, HAS to be
the same distance "d"
since the boat went, stopped, and came back,
same distance "d"
took 3hrs for that though.... or 180 minutes

so... let's take a peekd at the d = rt
distance = rate * time


`\begin{array}{ccccllll} &distance&rate&time(mins) \\ &\textendash\textendash\textendash\textendash\textendash\textendash&\textendash\textendash\textendash\textendash\textendash\textendash&\textendash\textendash\textendash\textendash\textendash\textendash\textendash\textendash\\ upstream&d&10-r&45\\ downstream&d&r&180 \end{array} \\ \quad \\ \begin{cases} d=(10-r)(45)\\ d=(r)(180) \end{cases}\implies d=d\implies (10-r)(45)=(r)(180)`

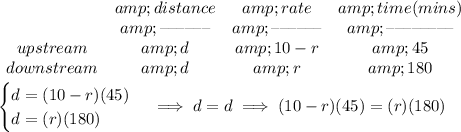
solve for "r"