Question

Casey says that a function exists if the input is a student's GPA and the output is the student's name. Is Casey incorrect? Why or why not?

A) Casey is incorrect because students can have the same name.
B) Casey is correct because more than one student can have the same GPA.
C) Casey is incorrect because more than one student can have the same GPA.
D) Casey is correct because it's unlikely that two students have the same GPA.

thankyou so much!!!

Answer 1

The answer is C. casey is incorrect because more than one student can have the same GPA

Explanation:

Answer 2

C) Casey is incorrect because more than one student can have the same GPA.

Explanation:

Casey states that there exists a function if we have,

Input = Student's GPA

Output = Student's name

Now, a function
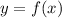`y=f(x)` is a relation where for each value of 'x', the value of 'y' is unique.

That is, for each input, there exists a unique output.

From the given statement, we have that,

A function exists if corresponding to every GPA, there exists only one student, which cannot be true.

There can be more than one students having the same GPA.

Thus, the correct option is,

C) Casey is incorrect because more than one student can have the same GPA.