Question

Suppose that the number of cells in a tumor doubles every 5 months. Considering that the tumor begins with a single cell, answer the following: How many cells will there be after 3 years? 5 years?

Answer 1

Let's call a 5-month period a "pent", so the conversion from years to pents is 1 year for every 2.2 pents.

Then


`3\text{ years}*\frac{2.2\text{ pents}}{1\text{ year}}=6.6\text{ pents}`

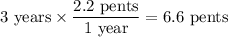
and


`5\text{ years}*\frac{2.2\text{ pents}}{1\text{ year}}=11\text{ pents}`

Now, if the number of cells doubles every pent, and if
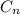
`C_n` denotes the number of cells after
`n` pents, then the number of cells is modeled recursively by


`C_(n+1)=2C_n`

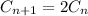
starting with
`C_0=1`.

Solving explicitly for
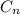
`C_n`, you arrive at


`C_(n+1)=2C_n=2^2C_(n-1)=2^3C_(n-2)=\cdots=2^(n+1)C_0`

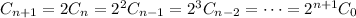
or,


`C_n=2^nC_0=2^n`

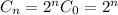
So, after 6.6 pents (3 years), you should expect the number of cells to grow to about
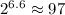
`2^(6.6)\approx97`. After 11 pents (5 years), you should find
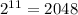
`2^(11)=2048` cells.